Author: l-sgn

Dynamical systems in general (numerical simulations and analytical methods)

•  computer assisted perturbation theory in general mathematical problems ([M1], [M2]) applied to the Sitnikov problem ([M3], [M4]), Trojan asteroids [M5], [M6], the spin-orbit problem [M7], [M8], [M9], and the motion of dust in our solar system ([M10], [M11], [M12])
• symplectic mapping methods in general mathematical problems (M13]), applied to the Lagrange problem ([M5], [M14], [M15], [M16]), and the Cassini state problem ([M17])

Celestial Mechanics (motion of celestial bodies in space)

• Orbital motion of asteroids ([A1], [A2], [A3], [A4]), dust ([D1], [D2], [D3]), the planets ([P1]), space debris ([D2]), and the Sitnikov problem ([S1], [S2], [S3], [S4])
• Rotational dynamics of asteroids ([A5], [A6], [A7], [A8]), comets ([C1]), planetary moons and planet Mercury ([P1], [P2], [P3])

Phase space portraits reveal the underlying structure of dynamical systems. The figure shows different types of orbits crossing a surface of section. An orbit at rest passes the section through an equilibrium point. A periodic orbit in blue regularly visits the center of resonant islands. A quasi-periodic orbit forms an invariant closed curve. These kind of orbits form regular structures on the surface of section, and their evolution into the past or future can be easily predicted. On the contrary, the next intersection point of the chaotic orbit in magenta is difficult to predict. It lies within a chaotic see of irregular structure on the section.

The figure was created using Wolfram Mathematica and was first published in a review article about the Sitnikov problem. See also my Scholarpedia article.

Micrometer sized space dust falls in two distinct categories of origin: natural and man-made. While natural space dust is formed in interplanetary space by means of cometary activity and asteroid collision, the man-made counterpart is mainly found in the near Earth environment. The origin of micrometer-sized space dust in the latter case is due to fragmentation of larger particles into smaller ones. Fragmentation is caused by collision and erosion of artificial satellites that have been placed in Earth-orbit to fulfil civil and military missions for human mankind. Television and communication services rely on satellites in the geostationary orbit, where the orbital period of the satellite coincides with the rotation period of the Earth. In my work on the long-term stability of micro-meter sized space debris in the vicinity of the geostationary orbit I investigated the role of the so-called Poynting-Robertson effect on the orbital motion of micro-meter sized space debris: the relativistic interaction of photons with micron sized space dust causes loss of orbital energy of the particles. As a result the semi-major axes, i.e. the distance from the centre of the Earth shrinks with time too. As a consequence micro-meter sized space dust of large amounts is able to pollute lower regimes of motion in the near Earth environment with time. High velocity impacts of these sub-millimetre sized objects with space crafts or astronauts in extravehicular activity may cause severe problems, like drop outs of electronics or even damage of space-suits with fatal consequences. For this reason special care needs to be taken in the design and choice of materials that are used in space industry to prevent such catastrophic events. It is therefore also a mandatory and crucial task to provide engineers with precise estimates of the amount and long-term fate of sub-millimetre sized space dust in the different Earth environments.

The figure was first published in [I], [II] and shows the inward drift in semi-major axis due to the Poynting-Robertson effect on the abscissa versus the initial distance of a dust grain released in the vicinity of the geostationary resonance. The blue line provides the estimate on the basis of an analytical theory. Red circles and black crosses mark averaged drift rates based on numerical simulations including the effect of the Moon. We notice that temporary capture of dust grains inside the 1:1 resonance with the rotation of the Earth may prolong the orbital life-time of micron sized dust grains significantly (see also my study in the Lagrange problem). Outside resonance the theory perfectly predicts the averaged drifts rates obtain from numerical simulations.

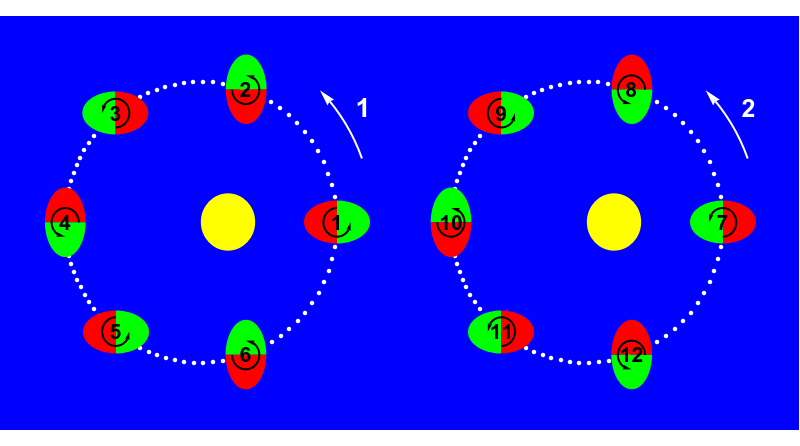
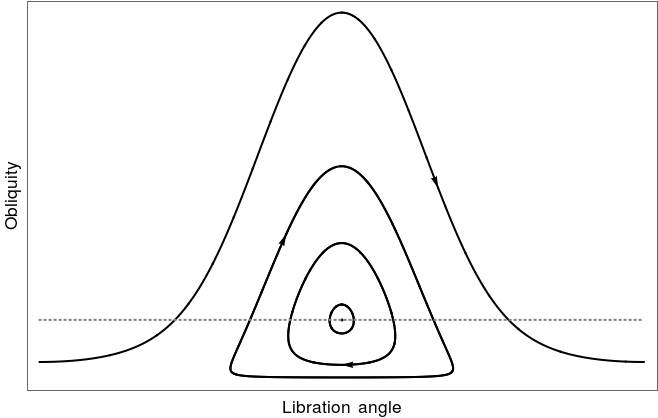
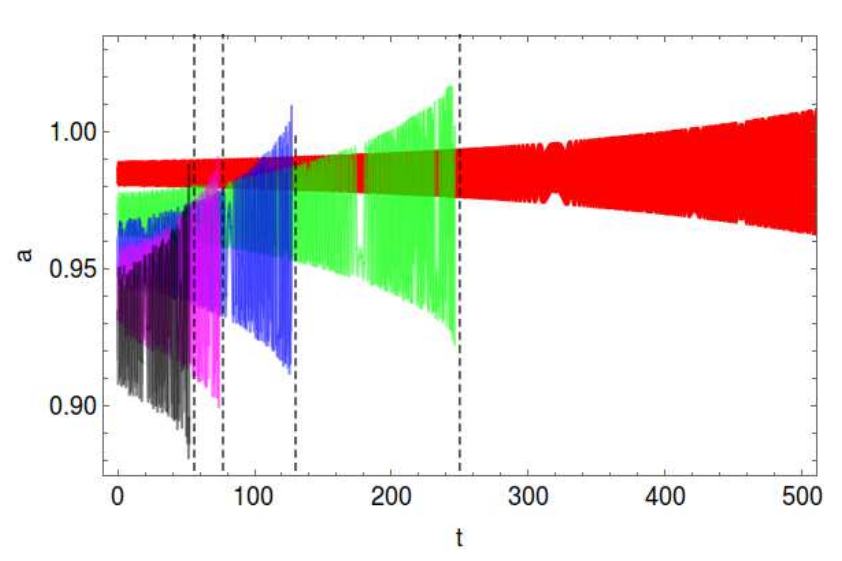
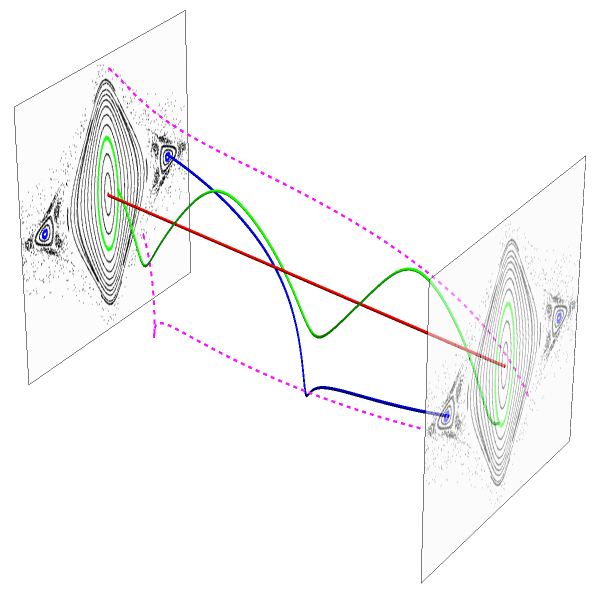
Motion of space dust close to the equilateral Lagrange points is determined by the gravitational attraction of the central star and the perturbing planets, but is also subject to non-gravitational forces, mainly due to the central celestial body. In my study on the phenomenon of temporary capture of space dust inside the orbits of the planets I investigated two main effects: the solar wind and drag due to the Poynting-Robertson effect. The latter effect describes the interaction of dust grains with photons by means of special relativity. It causes a drag term in the equations of motion of the dust grain in its first order Newtonian approximation. The term depends on the velocity of the dust grain and reduces the orbital energy of the grain. The same holds true for the drag term induced by the interaction of the dust grain with stellar winds.  As a consequence, dust grains in planetary systems spiral inwards, towards the central star on time-scales of the order of thousands of years, depending on the grain size and strength of stellar radiation.  However, it is known that temporary capture of dust grains in mean motion resonances with the planets may prolong the orbital life-time significantly.  While the stabilizing effect of the much weaker outer and inner resonances with the planets was already well understood, the effect of the much stronger 1:1 resonance remained unclear. With my study the scientific gap could be filled: stable motion for dust sized particles is not possible due to the Poynting-Roberston also in the equilateral configuration of the 1:1 resonance while temporary capture is possible for a wide range of system parameters. Much more important, the effect shifts the locations of the Lagrange points, and moreover may cause an asymmetry between the two Lagrange points L4 and L5 and may therefore also serve as an explanation for the observational evidence that the number of asteroids – if formed from dust in 1:1 resonance with a planet – is unequal between those two locations.

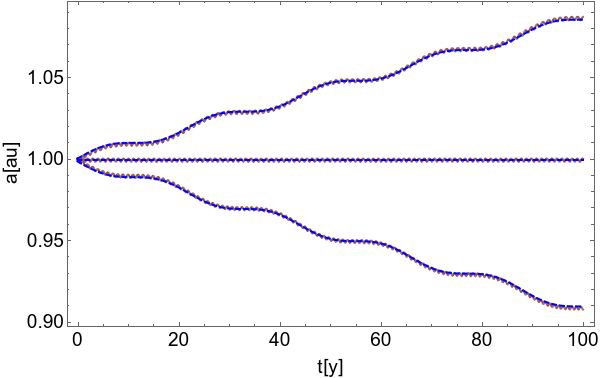
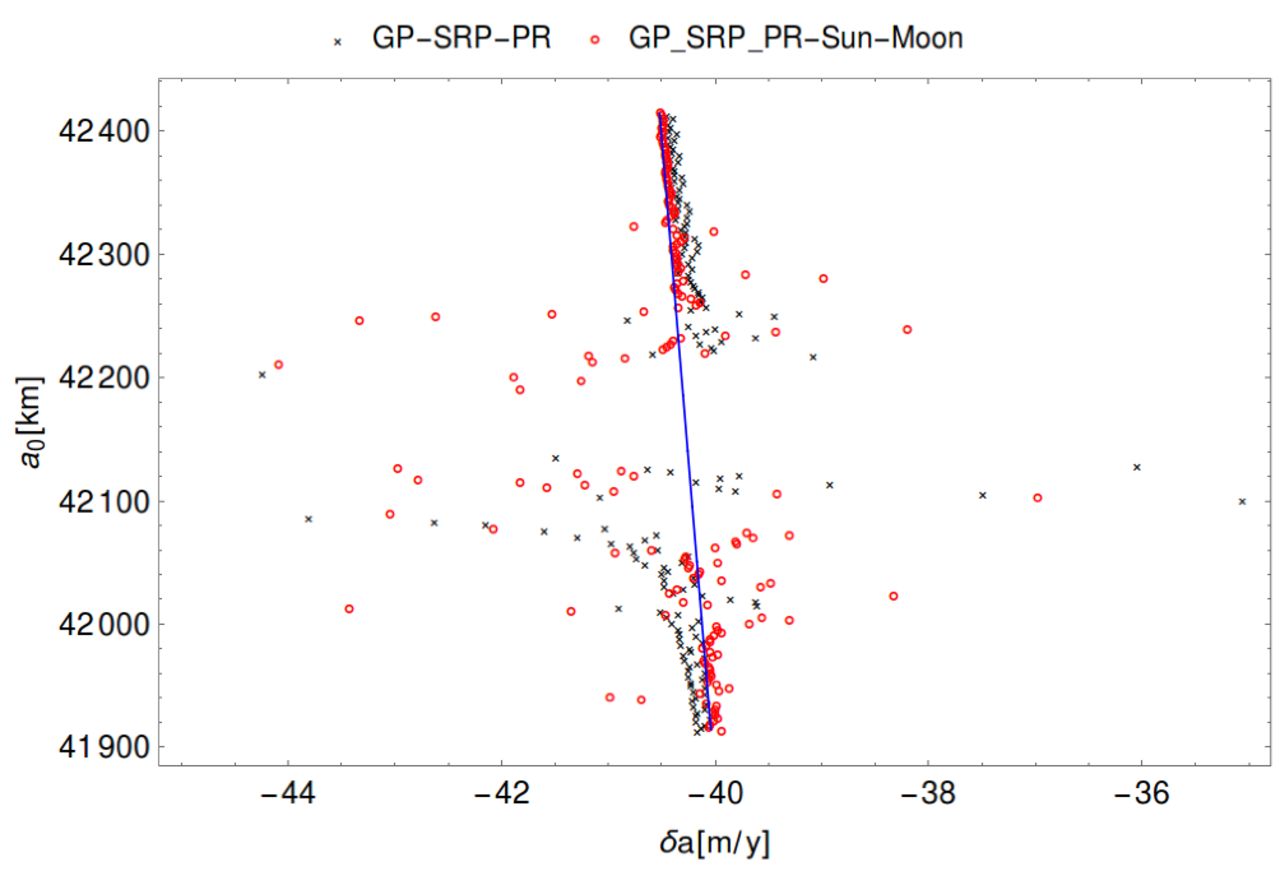
The figure was fist published in (1, 2) . It shows the phenomenon of temporary capture of space dust in 1:1 resonance with a planet that is located at 1 astronomical unit (see ordinate). One clearly sees the effect of temporary capture in terms of the oscillations around a mean value that defines the location of the resonance. While for extended celestial bodies the location lies also at 1 astronomical unit, the location is shifted to smaller values in semi-major axis due to the Poynting-Robertson effect. The stronger the effect the larger the shift, and the smaller the time of temporary capture.

Micro-meter sized dust grains in the heliosphere are not only subject to the gravitational attraction due to the other celestial bodies like the sun or the planets, but also experience a force due to solar radiation, and the inter-planetary magnetic field. While the interaction with photons and the solar wind may cause the grains to spiral towards the sun, the interplanetary magnetic field may counteract this kind of motions. In my study on the dynamics of charged dust grains in the heliosphere I derived a simple theoretical condition on the charge-to-mass ratio for which the distance from the central star becomes stabilized. The relation is used to demonstrate that the orbital life-time of dust grains in the solar system may drastically be prolonged in presence of normal components of the interplanetary magnetic field.

The figure shows the evolution in time of the distance of the dust grain from the sun in astronomical units for three different values of the charge-to-mass ratio: for uncharged grains the distance decreases with time and the grain will eventually fall back into the Sun; for charged particles, with arbitrary charge large enough the grain’s distance from the Sun increases with time. Only, if the charge-to-mass ratio fulfils certain criteria explained in full detail in (1) then the semi-major axis of the dust grains remains at its initial value over the full time period.

Normal forms of dynamical systems allow to investigate special solutions and their nearby phase space geometry in an easy and concise way. Dynamical systems usually follow from the statement of a physical problem in some set of coordinates. The choice of coordinates often resembles the point of view of the observer of the problem. From the point of view of the theoretician those coordinates are usually not the best ones to investigate the problem. Better coordinates are chosen to transform the dynamical system into a form that allows to better understand the underlying structure of possible solutions and the phase space geometry. Canonical variables are the right choice to tackle dynamical problems that can be derived from a potential or admit a Hamiltonian function. Sophisticated mathematical tools have been invented over the last centuries to understand the nature of such systems, and to reveal the hidden secrets common to most dynamical problems found in physics. One major topic concerns the stability of motions, i.e. the stability problem. Roughly speaking, one seeks to find conditions on the parameters space and initial state of motions that allow stable solutions over long times. I have used normal forms to investigate stability of motions in various research studies over the past years, close to the triangular Lagrange points in a mapping of the restricted three-body problem or in the spin-orbit problem (1,2). For a review of the stability problem in generic dynamical systems, see Chapter 4 of my book.

In my work (I, II) on normal forms of weakly dissipative dynamical systems I generalized normal form theory to a class of dynamical systems that cannot be derived from a Hamiltonian function. The new theory was successfully applied to special classes of dynamical systems and allowed to state theorems about the stability of motions for different categories of initial states and system parameters for dynamical problems.

Asteroids are remnants of the violent formation process of our solar system. Some of these minor planets share their orbit with a major planet and are called co-orbital. The most common type of co-orbital objects we know are Trojan asteroids.  Trojans have been predicted by theory and  found by experiment – astronomical observations. In theory, there are special locations within the orbit of a major planet where the gravitational pull of the ‘major’ and the gravitational attraction of the central star – our sun – balance out each other in such a way to allow the motion of the ‘minor’ somehow ‘hidden’ within the orbit of the major planet. Observations show the existence of asteroids close to these points, but it remains open the question if the existence of these very interesting objects is just a temporary phenomenon or not. Many attempts have been made by scientists to answer this question. In my work on Nekhoroshev stability of Trojan asteroids I try to investigate the long term stability by means of a mathematical tool called Nekhoroshev stability. The aim of the study is to define a region close to the exact co-orbital configuration that includes asteroids which can stay within this region for time scales beyond the age of our solar system. It can be found and thus asteroids may also share their orbits with the major planets for very long times. This is a useful result to better understand the origin and formation process of planetary systems, i.e. our solar system that probably includes thousands of thousands of minor planets that have been formed together with the major planets at the beginning of our solar system.

The figure has been published in my article about the Nekhoroshev stability of Trojan asteroids already in 2008 and contains new scientific results of the core topic of my PhD thesis. It is one of my most cited scientific work so far. More of my work on co-orbital motions of asteroids and space dust can be found here.

This year I organized together with Prof. Rudolf Dvorak, head of the Astrodynamical Group at the Institute for Astrophysics, the 9th Humboldt Colloquium on Celestial Mechanics. The meeting took place in Bad Hofgastein from 19.03.2017 to 25.03.2017. Over 50 participants from 16 countries all over the world contributed to the meeting with scientific talks about recent progress in the field of Celestial Mechanics. Selected papers of the meeting will be published in the scientific journal CM&DA soon. We thank Hotel Winkler, the sponsors, the scientific and local organizing committees, and all participants for their efforts to make the meeting a big success.

In 2018 the space mission Bepi-Colombo will start its long-term journey to visit our innermost planet. It is Europe’s first mission to Mercury. The mission objectives include the investigation of the origin and evolution of planets very close to their parent star. I am interested in the orbital and rotational evolution of this planet. My article on the steady state obliquity of a rigid body has been published in CM&DA. In this work I investigated the influence of the gravitational field on the axial tilt and coupling between the rotation and orbit of planet Mercury. The axial tilt, or obliquity, of Mercury is close to but not exactly zero, and the orbital period of Mercury is about 88 days while the rotation period is very close to 2/3 of this value. Mercury therefore is currently situated in a 3:2 spin-orbit resonance with non-zero obliquity. The magnitude and stability of the axial tilt is determined by the kind of spin-orbit resonance and the gravitational field, i.e. the internal mass distributions of the planet. Mercury, very probably, was not always situated in the 3:2 spin-orbit resonance. Formation studies of the planets assume that planets form at much higher rotation rates. Over time dissipative effects like tidal friction slows down the rotation period to allow the coupling between the orbit and the rotation of the planet. In my study I investigate the influence of different spin-orbit resonances and an extended gravitational field on the magnitude of the axial tilt. I derive simple formulas that allow to predict this steady state obliquity for given spin-orbit resonance and gravitational field parameters. I also derive a simple mathematical model that allows to investigate the oscillations of Mercury around exact spin-orbit resonance. The amplitude and periods of these oscillations are the result of other physical effects, i.e. the internal composition of Mercury.

I was invited speaker in the 7th International Meeting on Celestial Mechanics. The meeting took place in San Martino al Cimino, a beautiful village situated near the city of  Viterbo, Italy. I would like to thank the organizers for the kind invitation, and the organization of the meeting. My presentation took place in the Monday afternoon session, where I summarized my recent scientific findings on Cassini state 1. It has also been made available on youtube thanks to the organizers.

Cassini states correspond to special orientations of the spin axis of a celestial body. If the orbit of a celestial body gets perturbed then the orientation of the rotational axis of the body tries to keep its alignment with the normal axis of the orbital plane. The steady state solution corresponds to the point in the figure.  The closed curves surrounding this point correspond to solutions of the problem where the rotational axis starts oscillating around the steady state solution.

The figure was created using Wolfram Mathematica and was first published in my article of CM&DA. See also my related work (I, II) as a co-author done with Marco Sansottera and Anne Lemaitre, and Benoit Noyelles (III).